Transaction sandwiches

This is a brief analysis of the feasibility/effect of frontrunning of Bancor contracts.

Full disclosure: I have assisted in the implementation of the Bancorformula, and have performed security audits of the other Bancor contracts, on a consultancy basis on behalf of my company Dyno Security AB.

This analysis is my own independent research. If you find any errors or omissions, please let me know.

Frontrunning

Frontrunning can occur if I know you’re about to buy e.g. APPLE stocks for 1M USD (without a limit). Armored with this knowledge, I can then proceed to push the sell-side north by buying exactly 1M USD worth of AAPL.

Then I place my own sell-order, just below the last ‘untouched’ sell-order remaining on the sell-side. When your order hits the ‘floor’, it will immediately match against my sell-order, and you will do the entire buy at what would otherwise been the highest point.

Frontrunning is very old. According to Wikipedia, the term originates from the era when stock market trades were executed via paper carried by hand between trading desks:

The routine business of hand-carrying client orders between desks would normally proceed at a walking pace, but a broker could literally run in front of the walking traffic to reach the desk and execute his own personal account order immediately before a large client order

It is still very much a problem these days, and the reason why HFT trading can earn huge gains simply by being faster than the ‘regular route’.

It’s the reason why a 300 M$USD trans-american fiber line from Chicago to New Yersey was secretly built in 2008, and why exchanges make huge profits each year from co-location whereby HFT-firms can rent space closer to the matching-engines.

Frontrunning on the blockchain

In the classical example; frontrunning is “Buy X, then turn around and sell X” (or vice versa). On the blockchain, the scenario is a bit different. I’m going to look at the Bancor model.

In essence:

A buy causes the price to go up
A sell causes the price to go down.

Here’s a graph of the return from buying 100 Ether worth of tokens. I used the start-parameters of the BNT/ETH market.

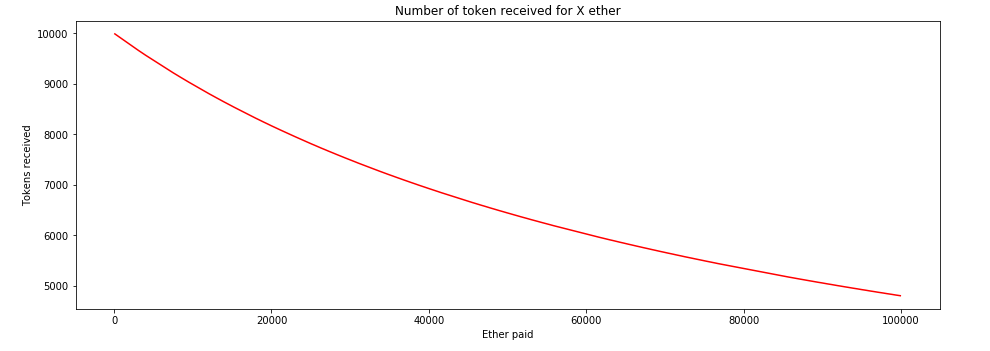
As you can see, the price is initially cheap, returning 100 Tokens per ether, and then the return gradually eases down towards nothing.

On the blockchain, all transactions will be visible on the network for a certain amount of time before it’s included in a block. Since the Ethereum blocktime is ~16s (the winter is coming), there is ample time for an attacker to see and react to an order.

In the Bancor-model, the execution of frontrunning is different compared to the ‘classic’ example, with respect to the ordering. Here’s how it would look:

See a buy of 100 Ether
Perform a buy of 100 Ether
Allow original buy of 100 ether
Sell tokens received in 2.

Since there’s a guaranteed price-rise when the original order goes through, there’s a guaranteed win to purchase first, bump the price, and then sell the purchased tokens.

The attacker is not restricted to the same magnitude of order as the original buyer, and we’ll look at that scenario aswell.

Prerequisites for an attack

The one actor which most easily can perform a frontrunning (sandwiching) is a miner, since only a miner can decide on the order of transactions within a block.

A regular user could, with some luck, perform a sandwiching if the stars are correctly aligned (not too many other transactions, instrumentation of gas prices, and no other interfering buys/sells) - but it could just as easily backfire if the transactions were carried out in the wrong order, or split into different blocks.

The other prerequisite is that the order is a ‘Market’ order. In the Bancor-model, that means that the parameter minReturn have been set very low.

Note: The minReturn cannot be 0 - that is forbidden by the contract, to force users into explicitly specifying a lower bounds on acceptable return.

Frontrunning in practice

Let’s look at how that works in reality. Let’s choose somewhere in the middle of that graph, say after 20K ether has been put in.

Sandwiching after 20K ether already bought

Attacker got 8162.568177611280925848 tokens
Victim got 8155.171936770836842343 tokens. Loss 7.396
Attacker got 100.089541406713207624 Ether

So out of the original 100 Ether, the attacker now got 100.09 ether, or 0.09% ROI.

Meanwhile, the victim obtained 8155.17 Tokens, losing out roughly 7.4 tokens on the attack.

Let’s look at the same attack lower in the range, e.g. before any other buys have been performed.

Sandwiching at original price

This is the case where we’re on the left side of the graph, which ought to be more susceptible to this attack due to the steeper slope of the graph.

Attacker got 9991.776063567493110895 tokens
Victim got 9980.455634510765501270 tokens. Loss 11.320
Attacker got 100.112545806806910495 Ether

Better - the attacker now got 100.11 Ether, a ROI of 0.1%. The victim, meanwhile, obtained 9980.46 Tokens, instead of 9991.78 - losing out on 11 tokens.

Griefing frontrunning in practice

There’s something else that the attacker can do aswell, which is griefing. Instead of sandwiching the original order with orders of the same value, he can he can submit gigantic buys/sells.

This will temporarily move the market way over to the right side of the graph, severely punishing the original buyer.

Let’s assume the attacker has 100K Ether, and see what he can do. We’ll do both cases of ‘20k Ether in’ and ‘original price’.

Also, note that this is far from risk-free for the attacker, as we’ll see further down.

Griefing with 100K Ether after 20K ether already bought

This is again the case where we’re a bit in, but still on the left side of the graph.

Attacker got 5851455.493106751074013682 tokens
Victim got 4362.217293956048971654 tokens.
Attacker got 100046.567914623968472200 Ether

In this case, the victim obtained a mere 4362 tokens, losing (8155- 4362) 3793 tokens in the attack, close to half the value.

The attack ended with 100046 ether for the attacker - a gain of 46 Ether, a ROI of 0.046%.

Griefing with 100K Ether at original price

This is the case where we’re on the leftmost side of the graph.

Attacker got 6740068.426828138064593076 tokens
Victim got 4797.581116555070694402 tokens.
Attacker got 100051.997708364649024530 Ether

In this case, the victim obtained 4797.60 tokens instead of 9991.78: more than 50% (5194) tokens were griefed.

The attacker, meanwhile, netted 51 ether, or ROI of 0.051% by performing the griefing. This is a lower ROI percentage-wise, but a higher absolute.

Attacker risks

There are two risks that the attacker is forced to take, both for the ordinary sandwich and the griefing sandwich; one obvious risk and one a bit less obvious.

The obvious risk is that the extra processing time (detecting opportunity, calculating values, signing two transactions) delays the start of mining the new block, and increases the uncle-rate for the miner.

The less obvious risk is that the miner can be counter-attacked by other miners. When the miner Mallory releases his block, it will have the following transactions, in this order (I’m assuming that Mallory sets minPrice):

User Mallory -> buy 100K ether worth of Tokens (N tokens at price X)
User A -> buy 100 ether
User Mallory -> sell N tokens (at price Y)

Now, as soon as Mallory releases the block b above, there’s a risk that it get’s included as an uncle, and not on the main chain. If that happens, another miner (Sniper)can see that the two transactions 1) and 3) are not in the main chain, and can pick them out from the uncle-block and include in a main block instead!

The next miner can choose to play them in the following order:

User Mallory -> buy 100K ether worth of Tokens (N tokens at price X)
User Sniper -> sell X tokens

The miner Sniper, if he is holding tokens, can take the opportunity of the failed griefing-attempt, and unload tokens at way above market price, during the temporary spike that Mallory intended to trap A to buy into.

Also, the replaying of “hidden” transactions revealed in uncled blocks does not necessarily have to be done by another miner; a anti-griefing resistance group could spot the sandwich-attempt and broadcast 1) on the network, to cause problems for the miner.

A Theorem

I think this can be generalised into a rule:

Any (miner-) attack which depends on transaction ordering and transaction secrecy, can be counter-attacked through information leaked in uncled blocks.

Because in any such attack, the transaction which have been kept from the network can be included in a different order in the main chain once the attack has failed, through uncling. Note, though, that naturally nonce-sequences cannot be included out of order, so when I say “out of order”, I mean the order between victim and attacker transactions.

Summary

Market orders are dangerous things. This is not something unique to ‘blockchain’; it’s inherent in the order type. An order of type ‘Market’ means that any price is acceptible. So don’t use that order type unless any price is acceptible. Markets may move, whether through malicious attacks, legitimate order delays or sudden rushes.

Since there is no TTL on transactions, and since markets can move quickly, you should protect yourself against sudden market movements by setting minReturn on any token-exchange made.

The griefing-factor can have quite severe consequences for the victim, but there are also non-neglible risks for a miner when performing “frontrun-by-sandwich”, in particular if the miner attempts to perform a larger-scale griefing attack.

Appendix

References

A lot of info about microwaves can be found in the series “HFT in my backyard”.
Several books deal with the rigging of the market, and the rise of high-frequency trading. I recommend “Dark Pools” by Scott Pattersson, and the (controversial) “Flash Boys” by Michael Lewis.
Ethereum average block time at Etherscan
More about transaction inclusion latency at EthGasStation

Experimentation

If you want to experiment with these things, start up TestRPC - a JS-based EVM implementation good for local testing against evm bytecode:

$docker run -p 8545:8545 ethereumjs/testrpc:latest

The following python code has been used to experiment:

from web3 import Web3,RPCProvider
import math, json
import unittest

SOURCE='../solidity/contracts/build/'

class Market():

    def __init__(self, S,R,F):
        self.web3 = Web3(RPCProvider())
        abi = json.loads(open('%sBancorFormula.abi' % SOURCE).read())
        bin = open('%sBancorFormula.bin' % SOURCE).read()
        formula = self.web3.eth.contract(abi=abi, bytecode=bin)
        tx = formula.deploy()
        self.formula = formula(self.web3.eth.getTransactionReceipt(tx)['contractAddress'])
        self.S = S
        self.R = R
        self.F = F

    def buy(self,E):
        T = self.formula.call().calculatePurchaseReturn(self.S, self.R, self.F, E)
        if T > 0:
            self.R += E
            self.S += T
        return T

    def sell(self,T):
        E = self.formula.call().calculateSaleReturn(self.S, self.R, self.F, T)
        if E > 0:
            self.R -= E
            self.S -= T
        return E


M = 1000000000000000000
def originalMarket(initialBuy = None):
    S = 79323978 *M
    R = 79344* M
    F = 10
    m = Market(S,R,F)
    if initialBuy is not None:
        m.buy(initialBuy)

    return m

def strwei(n):
    return "%s.%s" % (str(n)[0:-18],str(n)[-18:])

def attack(title, m , victimSize = 100 * M, attackSize =  100*M):
    tokens = m.buy(attackSize)
    print ("### %s \n " % title)
    print("1. Attacker got `%s` tokens" % strwei(tokens))
    victim = m.buy(victimSize)
    loss = tokens - victim
    print("2. Victim got   `%s` tokens." % strwei(victim))
    winner = m.sell(tokens)
    print("3. Attacker got `%s` Ether" % strwei(winner))
    print("")

attack("Sandwiching after 20K ether already bought", originalMarket(20000 * M))
attack("Sandwiching at original price", originalMarket())
attack("Griefing with 100K Ether after 20K ether already bought", originalMarket(20000 * M), attackSize=100000*M)
attack("Griefing with 100K Ether at original price", originalMarket(), attackSize=100000*M)

2017-07-10

tweets

Tweets by @mhswende

favorites

Favorites